Wavefunction character

Electrons determine the properties of matter. They provide the chemical bonding between the atoms, and are responsible, e.g., for light absorption and emission (except for very low photon energies), magnetic behaviour or electrical conductivity.
Although being particles in principle, due to their small mass they are strongly delocalized and can be best described by wavefunctions, the solutions of the Schrödinger equation (or Dirac equation for heavier elements).
Knowledge of the electron wavefunctions therefore strongly helps to understand the properties of matter. Quantum chemistry has made huge progress in calculating such wavefunctions in the recent past; nevertheless experiments are still absolutely necessary to test these predictions.

Cluster are very interesting objects to study in this respect; they are still small enough to be studied by high level theoretical calculations, but large enough to already exhibit some properties close to that of the bulk.
Furthermore they can be studied experimentally with very high precision.

Simple metal clusters: electronic structure

Simple metal clusters (clusters made of metals close to the ideal case of a free electron gas, like alkaline or noble metals) in principle have a simple electronic structure. They can be seen as spherical boxes filled with some electrons, which occupy angular momentum eigenstates just like electrons in single atoms. This leads to a very simple electron density of states, which exhibits a "shell structure". This can be seen in the figure below, which exhibits the calculated density of states of an icosahedral Na309- cluster.

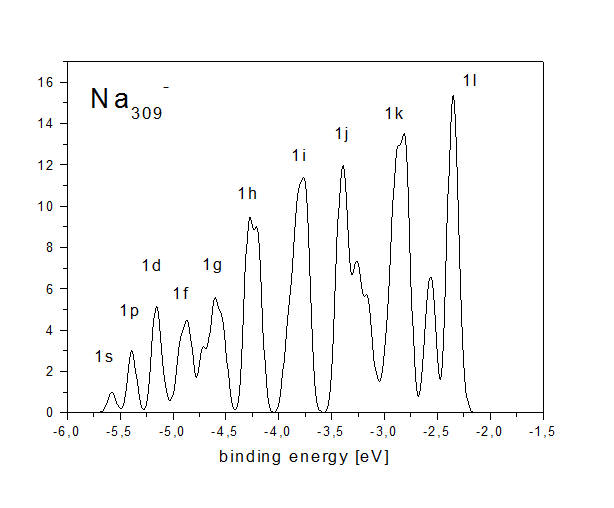
The approximate angular momentum quantum numbers of the states with radial quantum number 1 are indicated (there are also states with radial quantum numbers 2-5). One can see that the electron density of states is highly discretized; in this respect even this rather large cluster is far from being a bulk-like system with a continuous density of states.
The angular momentum assignment has to be called approximate as angular momentum is well defined only in systems with spherical symmetry. The icosahedral cluster is only approximately spherical; therefore angular momentum is not good quantum number. This can be see looking at the photoelectron spectra of copper and silver clusters shown below.

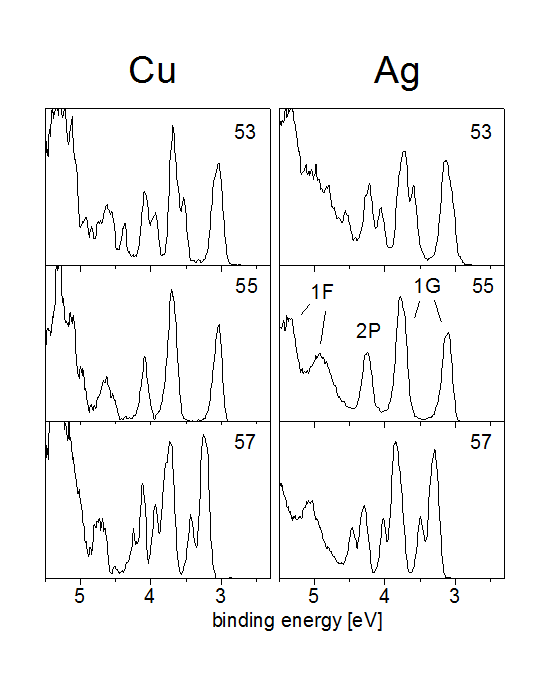
Both Ag55- and Cu55- clusters have icosahedral symmetry. This has an interesting effect on the electronic states. One can see that both states 1F and 1G split up into two states each. The reason is that icosahedral symmetry allows only maximally fivefold degenerate states; therefore the 1G state (l=4, so with (2l+1)=9 magnetic quantum number substates) has to split up into a fivefold and a fourfold degenerate state. The 1F with 7 substates splits up into a fourfold and a threefold degenerate state.
These new states are not angular momentum eigenstates anymore, but eigenstates of an icosahedral potential; in principle they could be strong mixtures of all kinds of angular momentum eigenstates.

Experimental characterization of the wavefunctions: angle resolved photoelectron spectroscopy

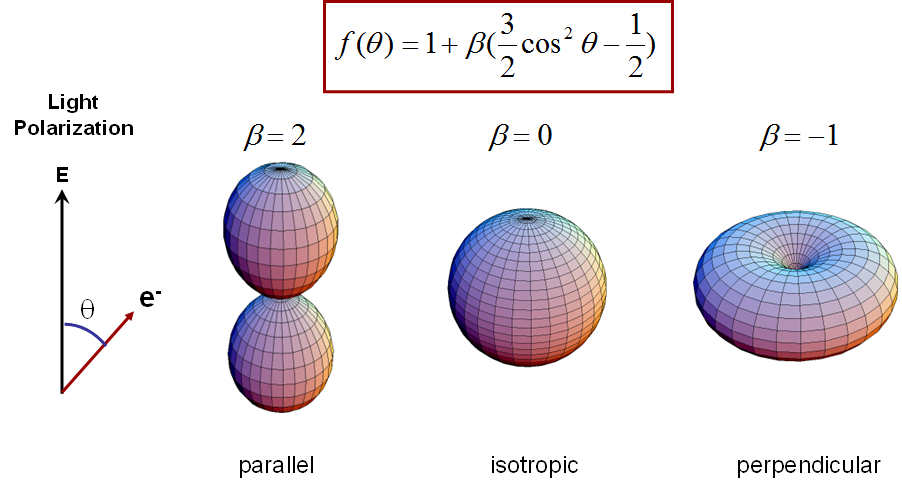
The angular distribution of photoelectrons strongly depends on the shape of their initial wavefunction. In solid state physics this is used to measure band structures, the energy of electronic states as a function of their k-vectors.

For molecules or clusters in free space the angular distributions are slightly less specific due to the averaging over all possible orientations of the particles. Nevertheless still a lot of information can be gained. Angular distributions of photoelectrons (with respect to the light polarization) from non-oriented clusters or molecules can be described by superpositions of squared sine and cosine functions, which can be parametrized by the so-called beta parameter (see below). This parameter takes values between -1 and 2 and describes distributions as shown below.

Using a VMI (velocity map imaging spectrometer, see instrumentation) we have measured angular distributions for a large range of cluster sizes, cluster materials and photon energies.
Examples are shown below.

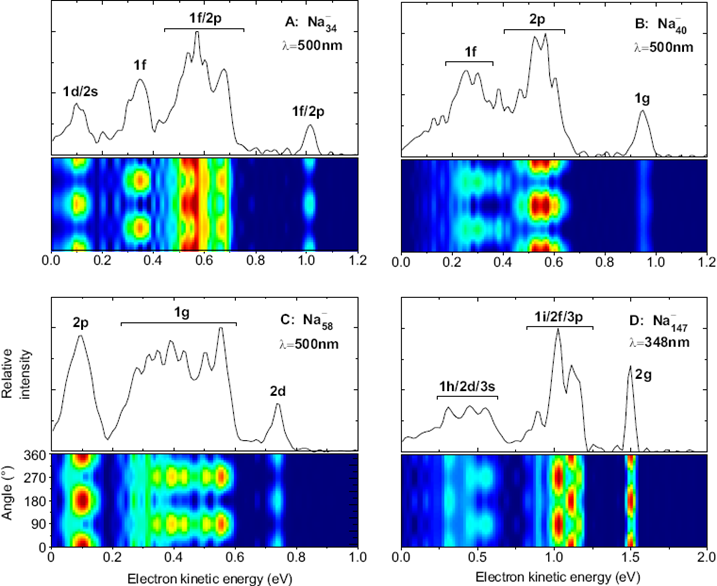
One can see that electrons emitted from different states exhibit very different angular distributions. These depend on photon energy, so we have repeated the measurements for a broad range of energies. In order to show the results, the distributions of electrons from certain states have been fitted to extract a beta parameter; this can then be shown as a function of photon energy, or final electron kinetic energy. An example is shown below.

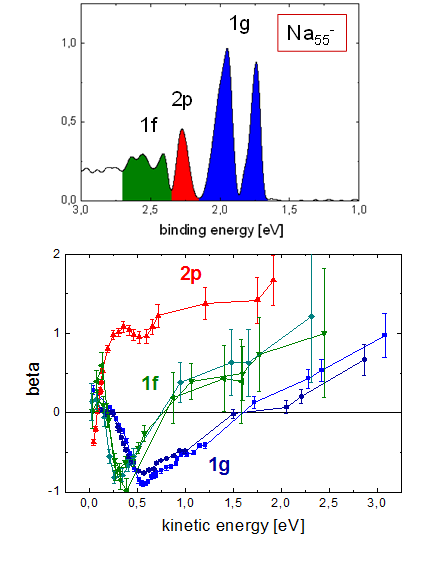
These are the beta parameters for electrons from four different states in a Na55- cluster, with approximate assignment 1g, 2p and 1f.
Two observations can be made immediately: the beta curves for different initial approximate angular momentum are very different, and almost identical for the substates of a given approximate angular momentum state. So obviously the interaction with the ionic structure of the cluster leads to a splitting of the states, that is different energies, but the overall shape of the wavefunctions is conserved.

Further reading